Название: Вычисление обратной матрицы

Вид работы: реферат

Рубрика: Математика

Размер файла: 64.56 Kb

Скачать файл: referat.me-217907.docx

Краткое описание работы: Рассмотрим квадратную матрицу Квадратная матрица называется невырожденной , или неособенной , если её определитель отличен от нуля и вырожденной , или

Вычисление обратной матрицы

Вычисление обратной матрицы.

Рассмотрим квадратную матрицу

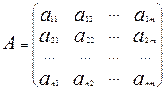
Квадратная матрица А называется невырожденной , или неособенной , если её определитель отличен от нуля и вырожденной , или особенной , если её определитель равен нулю.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение

АВ= ВА=Е ,

где Е – единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Матрица, обратная к А , обозначается через А^-1 , так что В= А^-1 . Для матрицы А обратная ей матрица А^-1 определяется однозначно.

Справедливы следующие равенства:

1) D (А^-1 )=( D А)^-1 ;

2) (А^-1 )^-1 =А ;

3) (А₁ А₂ )^-1 =А₂ ^-1 А₁ ^-1 ;

4) (А^Т )^-1 =(А^-1 )^Т .

Существую несколько способов нахождения обратной матрицы. Рассмотрим один из них – нахождение обратной матрицы путём вычисления алгебраических дополнений. Заключается он в следующем:

пусть нам дана матрица А , имеющая следующий вид:

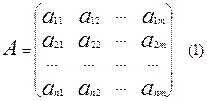
Предположим, что D А ¹ 0 . Построим следующую матрицу С следующим образом:

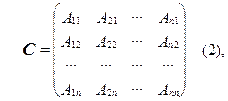
где А _ij – алгебраическое дополнение элемента а _ij в определителе матрицы А . Очевидно, что для построения матрицы С необходимо сначала заменить элементы матрицы А соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать.

Полученная таким образом матрица С называется присоединённой к матрице А , или союзной с А .

Чтобы получить матрицу А^-1 , обратную для матрицы А , необходимо каждый элемент присоединённой матрицы С поделить на D А , т.е. матрица А^-1 будет иметь следующий вид:

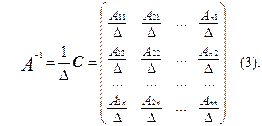
Пусть матрица А , имеет следующий вид:

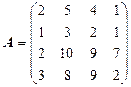
Чтобы найти матрицу А^-1 , обратную для матрицы А , необходимо:

- вычислить определитель матрицы (D А= -3 );

- найти алгебраические дополнения элементов а _ij в определителе матрицы А :

- составить присоединённую матрицу С по формуле (2);

- разделить все элементы матрицы С на D А .

Реализуем вышеизложенный алгоритм нахождения обратной матрицы следующим образом: вначале запишем в редакторе Word присоединенную матрицу С по формуле (2), после чего в программе Excel найдём обратную матрицу А^-1 (по формуле (3)) для матрицы А .

1. Включите компьютер.

2. Подождите пока загрузится операционная система Windows , после чего откройте окно Microsoft Word .

3. Вставьте объект Microsoft Equation 3 . 0.

4. Перепишем алгебраические дополнения в формульный редактор. Для этого:

·запишите алгебраическоедополнение А₁₂ ., используя шаблон нижних индексов;

·вставьте шаблон определителя 3-го порядка в формульном редакторе;

·занесите числовые значения определителя в свободные поля;

Повтором предыдущих действий, запишите в редакторе формул дополнения А₁₂ -А₄₄ (см. рис. 8.1)

В качестве вычислительного средства воспользуемся инструментами программы Excel .

5. Откройте окно Microsoft Excel .

6. Перепишите матрицу А и формулу (4) из Word в Excel (см. рис. 8.2).

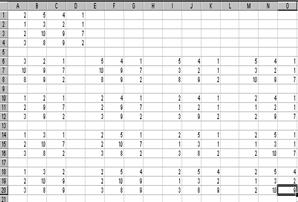
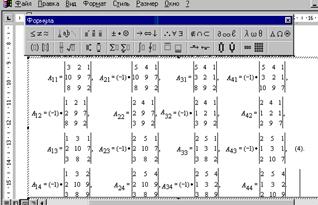
Рис. 8.1 Рис. 8.2

7. Используя функцию МОПРЕД, которая находится в мастере функций ƒ_х , посчитаем, чему будут равны все алгебраические дополнения. Для этого:

·активизируйте ячейку D9;

·выполните нажатие ЛКМ на кнопке ƒ_х в стандартной панели задач;

·в окне КАТЕГОРИЯ нажатием ЛКМ выберите МАТЕМАТИЧЕСКИЕ, а в окне ФУНКЦИЯ – МОПРЕД;

·выделите область A6¸C8;

·

Рис. 8.3

выполните нажатие ЛКМ на кнопке ОК (рис. 8.3).

Аналогичные действия проделайте со всеми остальными алгебраическими дополнениями, не забывая при этом некоторые из них умножать на число (-1). В результате проделанных действий получим: А₁₁ = -45, А₁₂ = 20, А₁₃ =1, А₁₄ =-17, А₂₁ =63, А₂₂ = -31, А₂₃ =1, А₂₄ =25, А₃₁ = -6, А₃₂ =3, А₃₃ =3,33Е-16, А₃₄ = -3, А₄₁ =12, А₄₂ = -5, А₄₃ = -1, А₄₄ =5.

Как вы видите, значение дополнения А₃₃ записано в виде числа с мантиссой. Приведём это число к виду обыкновенной десятичной дроби. Для этого:

· активизируйте ячейку L17, после чего нажатие ПКМ;

· на экране компьютера появится контекстное меню;

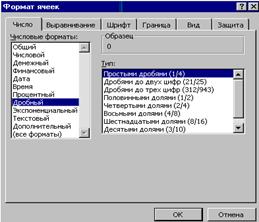
· выполните нажатие ЛКМ на слове ФОРМАТ ЯЧЕЕК (рис. 8.4);

Рис. 8.5

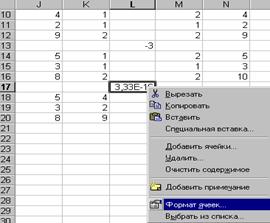
Рис. 8.4

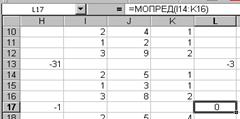·после появления диалогового окна ФОРМАТ ЯЧЕЕК в окне ЧИСЛОВЫЕ ФОРМАТЫ нажмите ЛКМ на ДРОБНЫЙ, а в окне ТИП – на ПРОСТЫЕ ДРОБИ (рис. 8.5);

·выполните нажатие ЛКМ на кнопке ОК . После чего алгебраическое дополнение А₃₃ =0 см. рис. 8.6

-Далее, в тексте задачника, если будут встречаться числа с мантиссой или бесконечные десятичные дроби, то будем пользоваться диалоговым окном ФОРМАТ ЯЧЕЕК, а данную операцию будем обозначать : поменяйте формат ячейки... на ДРОБНЫЙ.

8. Найдём в Excel матрицу А^-1 , обратную для А . Для этого:

·заполните ячейки А22¸D26 значениями алгебраических дополнений, используя формулу (2), т.е., в ячейках А23¸D26 записана присоединённая матрица С (рис. 8.7).

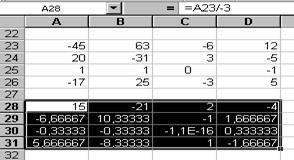
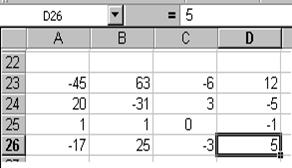
Рис. 8.7 Рис. 8.8

·активизируйте ячейку А28 и запишите с клавиатуры в неё формулу: =А23/-3, после чего результат занесите автозаполнением в ячейки В28¸D28; А29¸А31 и В29¸D31 (рис. 8.8).

·Выделите область А28¸D31, после чего поменяйте формат выделенных ячеек на ДРОБНЫЙ (см. рис. 8.9).

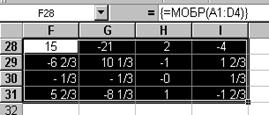
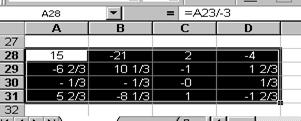
Рис. 8.9 Рис. 8.10

9. Проверку проделанных вычислений произведём следующим образом:

·выделите область F28¸I31;

·воспользуйтесь функцией МОБР, которая находится в мастере функций ƒ_х ( категория – МАТЕМАТИЧЕСКИЕ);

·на клавиатуре одновременно нажмите следующую комбинацию клавиш: Shift + Ctrl + Enter .

В результате чего в ячейках появятся следующие значения (рис. 8.10). Полученные значения доказывают правильность произведённых вычислений.

Задания для самостоятельной работы.

1)	2	2	-1	1	1	-0,5	0,5	-1	2)		3		4		1		2		6 1/3	-4 1/6	-2 1/3	2 5/6
4	3	-1	2	ответ:	1	0,5	-0,5	0	3		5		3		5		ответ:	-5	3,5	2	-2,5
8	5	-3	4	-1	1,5	-0,5	0	6		8		1		5		2	-0,5	-1	0,5
3	3	-2	2	-4	1,5	-0,5	2	3		5		3		7		0	-0,5	0	0,5
3)	2	3	11	5	- 2/7	2/7	5/7	- 1/7	4)		2	-2		0		1			1/4	1/6	0	0
1	1	5	2	ответ:	1 2/7	-2 4/5	2/7	- 1/3	2	3		1		-3			ответ:	- 1/6	0	0	1/8
2	1	3	2	- 1/7	2/3	- 1/7	0	3	4		-1		2			3/8	- 1/2	- 1/3	1 1/7
1	1	3	4	- 1/7	1/7	- 1/7	3/7	1	3		1		-1			1/8	- 2/5	0	4/9
5)	2	-2	0	1	1/4	1/6	0	0	6)		2	5		4		1			1	- 1/3	- 1/2	1/7
2	3	1	-3	ответ:	- 1/6	0	0	1/8	1	3		2		1			ответ:	- 4/5	1 5/7	0	0
3	4	-1	2	3/8	- 1/2	- 1/3	1 1/7	2	10		9		7			5/6	-2	1/5	0
1	3	1	-1	1/8	- 2/5	0	4/9	3	8		9		20			- 1/5	2/7	0	0
7)	1	1	-6	-4	- 1/9	1/4	0	0	8)		4	-3		1		5			1/2	0	- 3/5	1/3
3	-1	-6	-4	ответ:	2/5	- 1/4	0	0	1	-2		-2		-3			ответ:	1/2	- 2/9	- 8/9	2/5
2	3	9	2	- 1/9	0	0	0	3	-1		2		0			- 1/2	- 1/9	1	- 2/7
3	2	3	8	0	0	0	1/9	2	3		2		-8			1/5	- 1/9	- 1/4	0
9)	7	9	4	2	1	0,6	-2	1,4	10)		2	-1		-6		3			- 2/9	3/8	0	-1 1/6
2	-2	1	1	ответ:	0	-0,2	0	0,2	7	-4		2		-15			ответ:	0	1/4	- 1/3	-1 1/6
5	6	3	2	-1	-0,6	3	-3,4	1	-2		-4		9			- 2/7	1/8	0	- 1/3
2	3	1	1	-1	0	1	1	1	-1		2		-6			- 1/8	0	0	- 2/7
11)	6	5	-2	4	0	- 1/3	3/4	3/7	12)		3	-2		-5		1			0	1/4	2/5	0
9	-1	4	-1	ответ:	0	1/9	- 1/5	- 1/5	2	-3		1		5			ответ:	- 1/6	0	3/8	1/5
3	4	2	-2	- 1/6	1 2/7	-2 1/4	-1 1/4	1	2		0		-4			- 1/7	1/6	1/9	0
3	-9	0	2	0	1	-2	-1	1	-1		-4		9			0	0	0	1/9
13)	2	-3	3	2	0	0	0	0	14)		1	1		-6		-4			- 1/9	1/4	0	0
6	9	-2	-1	ответ:	0	1/6	0	0	3	-1		-6		-4			ответ:	2/5	- 1/4	0	0
10	3	-3	-2	2/3	1/2	- 1/7	- 1/3	2	3		9		2			- 1/9	0	0	0
8	6	1	3	- 1/2	- 1/2	0	1/2	3	2		3		8			0	0	0	1/9
15)	1	2	3	-2	0	1/9	1/6	1/9
2	-1	-2	-3	ответ:	1/9	0	1/9	- 1/6
3	2	-1	2	1/6	- 1/9	0	1/9
2	-3	2	1	- 1/9	- 1/6	1/9	0