Уравнение Пуассона. Его применение для расчета полей в вакууме

М.И. Векслер, Г.Г. Зегря

Уравнение Пуассона для ε = 1 выглядит:

(16)

Это уравнение - основа практических численных расчетов.

В задачах, решаемых аналитически, φ и ρ обычно зависят только от одной координаты. При интегрировании можно вычислять интегралы как неопределенные, не забывая выписывать +const, а затем отдельно находить эти константы. Если раccматриваются отдельные диапазоны координат, то на незаряженных границах необходимо "сшивать" потенциал: φ и - для вакуума - d φ/dx (или dφ/dr) не должны иметь разрыва. Если граница заряжена (σ), то dφ/dx испытывает скачок на величину –σ/ε0. Кроме того, если ρ и суммарный заряд конечны, то φ всюду конечен.

Другой вариант - сразу правильно писать пределы интегрирования. Для этого используется известное (или очевидное из симметрии задачи) значение поля () в одной какой-либо точке и значение потенциала в какой-либо точке (не обязательно в той же, где знаем поле). Если в задаче не оговорено иное, то следует принимать φ|∞ = 0. Так, например, для случая зависимости потенциала только от одной сферической координаты r

(17)

после переноса r2 в правую часть и двух последовательных интегрирований получаем:

	=		(18)
φ(r)	=		(19)

При этом взято φ|r = ∞ = 0 и учтено то обстоятельство, что при всюду конечном ρ поле в центре равно нулю (–dφ/dr|r = 0 = 0).

Задача. Пластина ширины 2a (ее ε≈ 1) заряжена равномерно по объему (ρ(x) = ρ0); при x = 0 (центр пластины) φ = 0. Найти φ(x).

Ответ: , |x|<a; , |x|>a

Задача. Пластина ширины 2a (ее ε≈ 1) заряжена как ρ(x) = α x2; при x = 0 (центр пластины) φ = 0. Найти φ(x).

Решение: Мы работаем в декартовой системе координат, причем очевидно, что и поле, и потенциал зависят только от x. Если ρ>0 (α >0) то поле - из симметрии задачи - направлено по оси x при x>0 и против оси x при x<0. Согласно уравнению Пуассона:

	=
	=	0 x>a или x<–a

После первого интегрирования (интеграл берем как неопределенный)

	=
	=	AL, x<–a
	=	AR, x>a

Неверным было бы записать одну общую константу для dφ /dx при x>a и x<–a. Второе интегрирование дает:

φ(x)	=
φ(x)	=	ALx+BL, x<–a
φ(x)	=	ARx+BR, x>a

Для нахождения шести констант у нас есть четыре условия сшивания (по два для границ x = –a и x = a). Кроме того, дано указание взять φ(0) = 0. Видно также, что Ex|x = 0 = –dφ/ dx|x = 0 = 0. Последнее очевидно из симметрии задачи. Отсюда сразу

Из симметрии следует также, что φ(x) = φ(–x) и что Ex(x) = –Ex(–x), вследствие чего

Это делает достаточным рассмотрение условий сшивания только на одной из границ, например при x = a:

	=	(ARx+BR)|x = a
	=	AR|x = a

Сначала получаем AR (AR = –α a3/3ε0), а затем BR (BR = α a4/4ε0), после чего остается выписать ответ:

φ(x)	=
φ(x)	=
φ(x)	=

Альтернативой было бы интегрирование с выписыванием пределов сразу:

Ex(x)	=
φ	=

Такое интегрирование верно всегда, в том числе при x<0. Точки x = ± a при этом ничем не выделены, но надо помнить, что вне участка –a<x<a ρ = 0 и учитывать это при подстановке плотности заряда в выражение для интеграла. После взятия интеграла в таком виде сшивание потенциала не требуется.

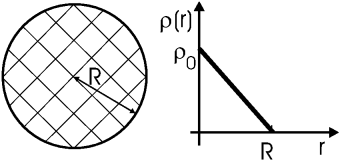Задача. Шар радиуса R заряжен как ρ(r) = ρ0(1–r/R). Найти полный заряд шара Q, поле Er(r), а также потенциал φ(r) при r = 0... +∞.

Решение: Полный заряд шара находится как

Q	=
=

При вычислении мы использовали выражение для элемента объема dV в сферических координатах (не следует смешивать фигурирующий при этом φ с обозначением потенциала). Уравнение Пуассона записывается:

=

Поcле однократного интегрирования в пределах 0... r имеем

	=
=

Заметим, что - с точностью до знака - мы уже получили поле, поскольку . Для нахождения потенциала φ(r) требуется повторное интегрирование:

r>R	: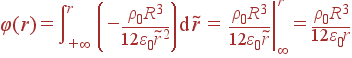
r<R	: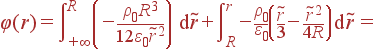
=

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.